问题模型

问题提出

有一个数组arr，下标从1到n，现在有w次修改，q次查询，修改的话是修改数组中某一个元素的值；查询的话是查询数组中任意一个区间的和。规模在50w左右

暴力解法

修改直接修改数组对应元素，时间复杂度为O（1），查询时直接相加，时间复杂对度O（n），总复杂度为O（wn).

前缀和解法

修改需要修改前缀和数组对应点后的所有值，时间复杂度为O（n)，查询时只需一次查询，时间复杂度为O（1），时间复杂度为O(qn).

可见暴力解法和前缀和解法时间复杂度其实大差不差.

寻找新解法

有没有一种做法可以综合一下这两种朴素做法，然后整体时间复杂度可以降一个数量级呢？有——树状数组。

树状数组思想

假设一个C数组，弃掉0下标不用，对于该数组每个下标所存内容，由如下规则决定：
将下标转为二进制表示，求出该二进制表示最低一个1所表示的值，记为lowbit：
该下标所存内容为arr数组中的(下标-lowbit,下标]的内容。
eg:6的二进制表示为（110），那么6的lowbit的二进制表示为10，即为2，所以下标6所存内容为arr数组中的（4,6]的和。

这样做的根据在哪里？我们以求前6项和举例：

$$\eqalign{ & \sum\limits_{{\rm{i}} = 1}^6 {arr[i] = (arr[1] + arr[2] + arr[3] + arr[4]) + (arr[5] + arr[6])} \cr & {110_2} = {100_2} + {10_2} \cr} $$

按照如上规则，我们分析C[4]所存内容，是不是如下：

$$\eqalign{ & \sum\limits_{{\rm{i}} = 1}^4 {arr[i] = (arr[1] + arr[2] + arr[3] + arr[4])} \cr } $$

C[6]所存内容，是不是如下：

$$\sum\limits_{{\rm{i}} = 5}^6 {arr[i] = (arr[5] + arr[6])} $$

所以：

$$\eqalign{ & \sum\limits_{{\rm{i}} = 1}^6 {arr[i] = C[4] + C[6]} \cr & {110_2} = {100_2} + {10_2} \cr} $$

也就是我们根据二进制拆分了前n项和，C数组的各种表示也由此而来。

lowbit求法

法一

思路

对x减1即可消掉二进制中最低的1个1，并且最低1所在位的后面所有位都会与原数对应位不同。

为什么不同？

答：考虑借位，由于在找到最低1前面，低位一直再向高位借1，一直借不到，所以所有的0会变为1，直到找到那个1，借1成功，1变为0.

再与原数x做与运算即可得到去掉最低位1的数，再用原数与其相减即可得到lowbit。

举例

6的二进制表示：
$${6_{_{10}}} = {110_2}$$
6-1二进制表示：
$${5_{_{10}}} = {101_2}$$
（6-1）与原数（6）做与运算：
$${101_2}\& {110_2} = {100_2} = {4_{10}}$$
原数与其相减：
$${6_{10}} - {4_{10}} = {2_{10}}$$
2即为所求。

代码

1
2
3
4
int lowbit(x) 
{	
    return x - (x & (x - 1));
}

法二

思路

结合求负数补码的方法。直接x&(-x)

举例

$$\eqalign{ & ( - {6_{10}}) = 1\_{0010_2} \cr & ( + {6_{10}}) = 0\_{0110_2} \cr & ( - {6_{10}})\& ( + {6_{10}}) = 0\_{010_2} = {2_{10}} \cr} $$

所以6&(-6)即为lowbit

代码

1
2
3
4
int lowbit(x) 
{	
    return x & -x;
}

树状数组实现

查询

思路

这里说的查询是查询任一区间的和，由于区间和具有可加减性，故转化为求前缀和：
查询前缀和刚刚在树状数组的思想中已经说过了，就是把大区间分成几段长度不等的小区间，然后求和。区间的个数为O(logn)，所以查询的时间复杂度为O(logn)。

代码

1
2
3
4
5
6
7
8
9
int getSum(int i) //i为下标
{
	int sum = 0;
	for (int k = i; k >= 1; k -= lowbit(k))
	{
		sum += crr[k];
	}
	return sum;
}

修改

思路

需要对被影响到的C数组元素都进行修改：

树状数组

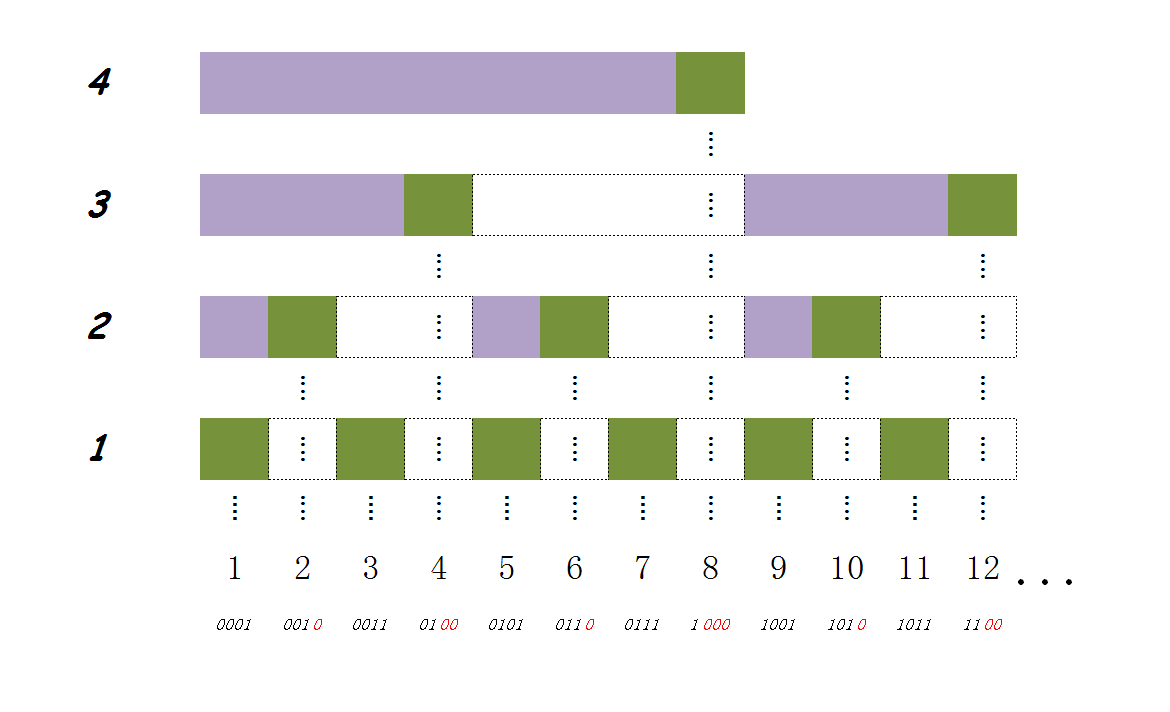
这就是C数组的含义，我们也由此可以得到一个性质：

  • 下一层后缀和只要补上自己后缀和的长度就可以得到上面层的后缀和

这个性质就是更新操作的依据，我们由此得到如下规则：

假设修改下标为x的内容，我们同时需要修改下标为：
$$\eqalign{ & x + lowbit(x) \cr & x + lowbit(x) + lowbit(x + lowbit(x)) \cr & ............. \cr} $$
直到超出我们所需要的边界n.修改的时间复杂度也为O（logn）

代码

1
2
3
4
5
6
7
void update(int i, int y ,int n) //位置为i,更新量为y,数目为n
{
	for (int k = i; k <= n; k += lowbit(k))
	{
		crr[k] += y;
	}
}

实战

题目背景

n个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是 0。
如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1，如果第二次要求他交换，则他的不高兴程度增加 2（即不高兴程度为 3），依次类推。当要求某个小朋友第 k 次交换时，他的不高兴程度增加k。
请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

输入描述

输入的第一行包含一个整数 n，表示小朋友的个数。
第二行包含 n 个整数,${H_1},{H_2},...$,分别表示小朋友的身高。其中：
$$1 \le n \le {10^5},0 \le {H_i} \le {10^6}$$

思路

对于这样的一个序列：
$$5,3,4,1,2$$
考虑中间的一般性情况，对于数字4代表的小朋友，他的交换次数取决于左边比他大的有多少，右边比他小的有多少，所以我们将身高作为C数组的下标,该身高的人数作为值，便加边查,从左边一次,重置后从右边一次,例如从左边边加边查查到4时,我们可以用getSum(4)得到当前加入的（5，3，4）中比4小或者相等的有2个，所以我们可以得到比4大的有3-2=1个，得到左边的值:1…依次类推我们可以得到每一位小朋友需要与左边的人交换的次数。

之后重置C数组,从右边加进来边加边查,可以得到每一位小朋友需要与右边的人交换的次数,两个加和可得每一位小朋友需要交换的次数。

代码

下标文中加1是因为身高会有0的情况，而C数组是弃0不同的,所以我们整体+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include <vector>
#include <cmath>
#include<algorithm>
#include<cstdlib>
#include <queue>
#include <set>
#include <sstream>
#include <cstring>
using namespace std;
int n;
int crr[10000005];
int arr[1000005];
long long cnt[1000005];
int lowbit(int i)
{
	return i & -i;
}


void update(int i, int y ,int n) //位置为i,更新量为y,数目为n
{
	for (int k = i; k <= n; k += lowbit(k))
	{
		crr[k] += y;
	}
}

int getSum(int i)
{
	int sum = 0;
	for (int k = i; k >= 1; k -= lowbit(k))
	{
		sum += crr[k];
	}
	return sum;
}


int main() 
{
	cin >> n;
	int maxH = 0;
	for (int i = 0; i < n; i++)
	{
		cin >> arr[i];
		if (arr[i] > maxH)
		{
			maxH = arr[i];
		}
	}
//左边
	for (int i = 0; i < n; i++)
	{
		update(arr[i] + 1, 1, maxH + 1);
		int sum = getSum(arr[i] + 1);
		cnt[i] = i + 1 - sum;
	}
	memset(crr, 0, sizeof(crr));
//右边
	for (int i = n - 1; i >= 0; i--)
	{
		update(arr[i] + 1, 1, maxH + 1);
		cnt[i] += getSum(arr[i]);
	}
//答案
	long long ans = 0;
	for (int i = 0; i < n; i++)
	{
		ans += (cnt[i] * (cnt[i] + 1)) / 2;
	}
	cout << ans << endl;
}